Financial Engineers at Mitsubishi UFJ Securities International Use Maple in Multi-asset Product Development

The latest release of Maple™ 12, the flagship product of Maplesoft™, offers quantitative finance professionals a platform for maximizing their productivity and efficiency. Maple’s powerful mathematical engine and sophisticated algorithms deliver a rich environment for modeling financial products and for process optimization.

When modelers, designers, or researchers alike turn to Maple for help in their theoretical research work or industrial applications development, their objectives are essentially identical to those faced by financial modelers,” said Igor Hlivka, Co-Head of Quantitative Analytics Group at Mitsubishi UFJ Securities International in London, who has used Maple in the financial industry for years. “Users look for a robust platform to design, solve, back-test, and visualize their product development tasks.

The greatest benefit of Maple is derived from the value its analytical tools add to financial product modeling. A symbolic solution to the product model, with its high computational speed and ease of implementation, is the most desirable outcome for a financial engineer. “In the world of financial options—probably the most advanced frontier in finance — analytical results are not always obvious, and testing for their existence can be a tedious and lengthy process. Employing Maple makes it very different; if a symbolic solution exists, Maple finds it quickly and correctly,” said Hlivka.

Hlivka recently developed a series of applications using Maple for multi-asset product development and for deriving semi-analytical solutions to non-standard options where multivariate stochastic processes play a determining role.

Application involving options with foreign exchange rate adjustment
Foreign exchange adjusted options enable investors to trade options on foreign assets without exposure to exchange rate risks. However, they introduce additional stochastic factors that extend the traditional univariate space into bivariate or multivariate space.

This application models the different methods used by market practitioners to adjust financial instruments and option valuations when payoffs are converted into different currencies. It demonstrates that changing the measure of probability is significant in finding solutions.

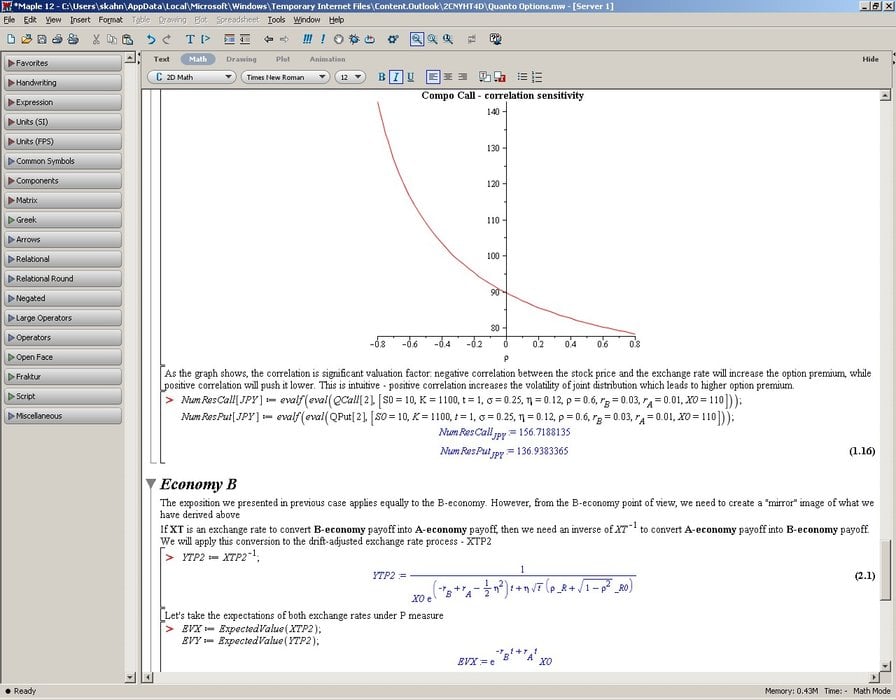
A key element is the use of Maple’s statistical functionality to model the volatility in the governing stochastic differential equations and the exchange rates, as well as the expected values. Additionally, Maple’s visualization tools are used to demonstrate that a negative correlation between the stock price and the exchange rate (which increases the joint volatility) increases the option premium, while positive correlation pushes it lower.

Application with Asian options
Contrary to the standard option contract, financial professionals may require exposure to an average value of an underlying asset over the whole life of a contract rather than its terminal value. These contracts, known as Asian options, are a more attractive tool for corporate treasurers and risk managers when they design hedging programs. Continuous geometric averages lead to a closed-form solution for an Asian option, and are the primary focus of this application. Although the application developed by Hlivka addresses stock prices, any lognormal dynamics can be valued easily with this approach.

In particular, Maple’s symbolic differentiation tools are used to generate a closed-form expression for the sensitivity of an Asian option to changes in the underlying stock price. The resulting expression indicates that the sensitivity is highest when the security price is close to the strike price, and is the most liable to change when the volatility drops to zero.

Perpetual options application
Unlike standard options, perpetual options have no fixed maturity and no exercise limits. This application uses Maple to solve the ordinary differential equations for their valuation. It also gives a closed-form solution for the stock price that maximizes the value of a perpetual put and call. This is done by differentiating formulas for their value, setting them equal to zero, and then solving for the stock price.

“I have worked with Maple on univariate processes on several occasions in the past, but have never tested its multivariate interface. It was a challenging and rewarding task,” added Hlivka. “Again, I gladly found Maple to be highly capable of handling these routines. Using various techniques related to the change of probability measure, I managed to get out of Maple a clear-cut and theoretically sound solution that logically presents and visualizes the sequence of steps, from model proposition to the final result.”

Multi-dependencies tend to be complex and difficult to model, but Maple makes this task more manageable, leading to practical predictive tools. With Maple, financial engineers can cope with these challenges well; the returned solution is quick, accurate, and intuitive. Moreover, the solution can be visualized easily for back-testing and scenario analysis.
Hlivka’s recent applications underline Maplesoft’s reputation as a powerful provider for financial engineers seeking fast, accurate, and easily deployable solutions to their daily product modeling needs.

  สอบถามข้อมูลเพิ่มเติม…